Combining resistances
There are two rules for adding the resistances of resistors in circuits, which are used depending on whether the resistors are in series or in parallel.
In a series circuit -
Where Rt is total resistance and Rn is the resistance of resistor n.
In order to derive the above formula, consider a series circuit with 3 resistors, with 3 different resistances, R1 , R2 , R3.
Using Ohm’s law, you can calculate the voltage across each resistor, as you know that the current flowing through each resistor is the same (Kirchoff’s first law).
Next, you can apply Kirchoff’s second law, which states that the sum of the voltages in a series circuit is equal to the supply voltage.
V = V1 + V2 + V3
You can replace each of the individual potential differences, (V1 etc.) using the equations from the first step.
V = IR1 + IR2 + IR3
Finally, factor out the current (I)
V = I(R1 + R2 + R3)
Notice that you have something that looks like Ohm’s law, except that the value of resistance is equal to R1 + R2 + R3 , meaning that this is the total resistance.
This can be extended to involve n many resistors in order to derive the general formula
In a parallel circuit -
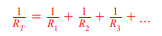
Where Rt is total resistance and Rn is the resistance of resistor n.
In order to derive the above formula, consider a series circuit with 3 resistors, with 3 different resistances, R1 , R2 , R3.
Due to Kirchoff’s second law, you know that the potential difference across each resistor is the same as the supply voltage. Using this and Ohm’s law, you can write 3 equations for the current across each resistor.
Due to conservation of charge, the sum of these individual currents must be equal to the overall current in the circuit (I).
This can be extended to involve n many resistors in order to derive the general formula.
You may need to use both of these rules when calculating the resistance of one circuit, for example: Find the resistance of the circuit in the diagram below.
Firstly, find the resistance of the parallel combinations of resistors:
Then, use the series rule to add the remaining two resistors to the value calculated for the parallel combination.
